The following example compares two MDS solutions for the well-known Ekman colour-perception data, derived from two different scaling programs. These data, which have frequently been used to illustrate non-metric scaling methods, are based on paired comparisons of stimuli in the form of light displays accross the visible spectrum, and are essentially two-dimensional. The solutions compared here, although originally superficially different in appearance, are shown to be practically identical in the first two dimensions, with minor differences occurring only in the third dimension, which has been included here for demonstration purposes. The third dimension can consequently be eliminated.
This example also illustrates a useful feature of multidimensional scaling conventions, namely that configurations are regarded as equivalent if they remain the same subject to what are here labelled "Similarity Transformations", which preserve the orderings of the distances between the points of which they are made up.
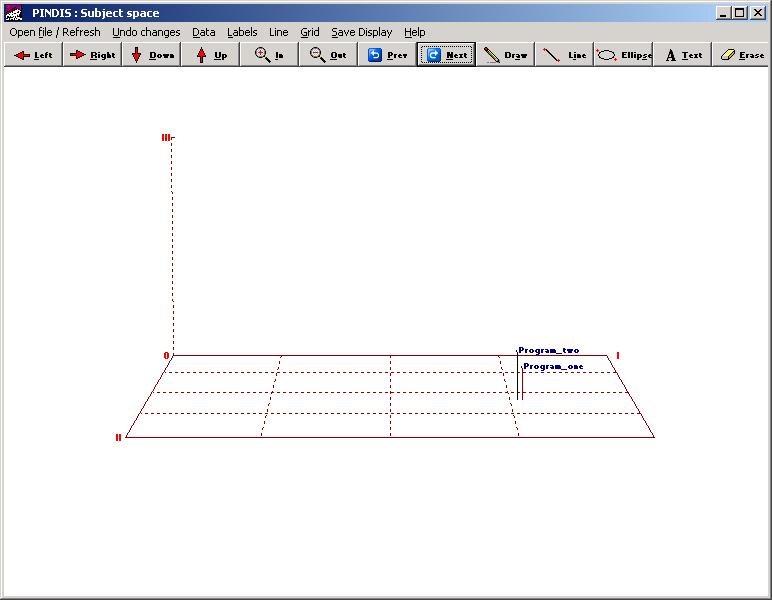
The 'subject space' looks like this :

Clicking on shows the following detailed information for the PINDIS analysis. This confirms the visual impression above, that the two solutions compared are practically identical.
------------------
Two scalings of the EKMAN data
Fit of Centroid Configuration
0.011047
0.011047
Centroid configuration
1 W434 -0.1103 -0.2149 -0.0606
2 W445 -0.1336 -0.1980 -0.0337
3 W465 -0.2596 -0.1139 -0.0091
4 W472 -0.2732 -0.0877 0.0290
5 W490 -0.2553 0.0726 -0.0097
6 W504 -0.1794 0.2087 -0.0026
7 W537 -0.0893 0.2443 -0.0886
8 W555 -0.0542 0.2685 0.0090
9 W584 0.1684 0.1666 0.0913
10 W600 0.2348 0.0818 -0.0210
11 W610 0.2660 -0.0339 -0.0172
12 W628 0.2564 -0.0975 0.0098
13 W651 0.2237 -0.1408 0.0117
14 W674 0.2057 -0.1557 0.0919
**** Perspective Origins ****
Subject
1 -0.1606 -0.2959 1.3429
2 0.0935 0.3574 -1.1140
**** Analytic Solutions for Individual Configurations ****
**** Configuration for Subject 1 ****
**** Program one
1) Similarity Transformations
Normed scalar for unconditional weights: 1.000000
1 W434 -0.1153 -0.2246 -0.0203
2 W445 -0.1322 -0.2022 0.0181
3 W465 -0.2582 -0.1100 -0.0423
4 W472 -0.2720 -0.0860 0.0154
5 W490 -0.2537 0.0735 -0.0430
6 W504 -0.1821 0.2123 -0.0276
7 W537 -0.0845 0.2515 -0.0706
8 W555 -0.0554 0.2622 0.0501
9 W584 0.1648 0.1619 0.0907
10 W600 0.2310 0.0802 -0.0202
11 W610 0.2718 -0.0362 -0.0180
12 W628 0.2590 -0.0930 0.0025
13 W651 0.2200 -0.1369 -0.0231
14 W674 0.2069 -0.1526 0.0883
Fit of subject to centroid/hypothesis --- S(Z,X) = 0.988953
2) Dimensional-weighting Transformations
Dimensional Weights:
1.0003 1.0025 0.7870
Dimensional Correlations:
0.9999 0.9996 0.8223
Fit --- S(ZW,X)= 0.990200
3) Perspective Models - Vector Weighting
Translation of Individual Configuration:
-0.0386 0.0313 0.1126
Stimuli: Vector Weights: Vector Cosines:
1 W434 1.0907 0.9916
2 W445 1.0845 0.9863
3 W465 0.9743 0.9946
4 W472 0.9928 0.9992
5 W490 0.9807 0.9951
6 W504 1.0011 0.9973
7 W537 1.0313 0.9983
8 W555 1.0336 0.9931
9 W584 0.9738 0.9999
10 W600 0.9644 0.9999
11 W610 0.9928 0.9997
12 W628 0.9648 0.9992
13 W651 0.8868 0.9915
14 W674 0.9694 0.9999
Fit --- S(VZ,X)= 0.992072
4) Joint Weighting Solution
Dimensional Weights:
1.0055 1.0075 0.8054
Vector Weights:
1 W434 1.0138
2 W445 0.9836
3 W465 0.9874
4 W472 0.9866
5 W490 0.9938
6 W504 1.0105
7 W537 1.0107
8 W555 0.9748
9 W584 0.9922
10 W600 0.9790
11 W610 1.0176
12 W628 0.9968
13 W651 0.9698
14 W674 1.0057
Fit --- S(VZW,X)= 0.990303
**** Configuration for Subject 2 ****
**** Program two
1) Similarity Transformations
Normed scalar for unconditional weights: 1.004231
1 W434 -0.1041 -0.2028 -0.1004
2 W445 -0.1335 -0.1916 -0.0851
3 W465 -0.2582 -0.1165 0.0241
4 W472 -0.2714 -0.0884 0.0422
5 W490 -0.2540 0.0709 0.0237
6 W504 -0.1747 0.2028 0.0224
7 W537 -0.0931 0.2344 -0.1057
8 W555 -0.0524 0.2719 -0.0321
9 W584 0.1701 0.1694 0.0908
10 W600 0.2360 0.0824 -0.0217
11 W610 0.2573 -0.0312 -0.0162
12 W628 0.2509 -0.1010 0.0171
13 W651 0.2250 -0.1431 0.0463
14 W674 0.2022 -0.1570 0.0945
Fit of subject to centroid/hypothesis --- S(Z,X) = 0.988953
2) Dimensional-weighting Transformations
Dimensional Weights:
0.9884 0.9864 1.2016
Dimensional Correlations:
0.9999 0.9996 0.9109
Fit --- S(ZW,X)= 0.990200
3) Perspective Models - Vector Weighting
Translation of Individual Configuration:
-0.0301 0.0329 0.1144
Stimuli: Vector Weights: Vector Cosines:
1 W434 0.8787 0.9832
2 W445 0.8866 0.9753
3 W465 1.0153 0.9965
4 W472 0.9965 0.9996
5 W490 1.0188 0.9957
6 W504 1.0021 0.9968
7 W537 0.9764 0.9988
8 W555 0.9708 0.9936
9 W584 1.0221 1.0000
10 W600 1.0283 1.0000
11 W610 0.9879 0.9994
12 W628 1.0108 0.9994
13 W651 1.0833 0.9945
14 W674 1.0051 1.0000
Fit --- S(VZ,X)= 0.992053
4) Joint Weighting Solution
Dimensional Weights:
0.9956 0.9902 1.1956
Vector Weights:
1 W434 0.9883
2 W445 1.0172
3 W465 0.9994
4 W472 1.0026
5 W490 0.9923
6 W504 0.9787
7 W537 0.9810
8 W555 1.0145
9 W584 0.9872
10 W600 1.0089
11 W610 0.9697
12 W628 0.9917
13 W651 1.0215
14 W674 0.9771
Fit --- S(VZW,X)= 0.990256
Normalized Dimension Weights
Subject Communality 1 2 3
1 0.9902 0.7701 0.6146 0.1397
2 0.9902 0.7609 0.6047 0.2134
Mean
Communality 0.9902 0.5860 0.3717 0.0325
--- Table of Subject Communalities for PINDIS Transformations ---
Transformation
Z,X[i] ZW[i],X[i] Z[i]W[i],X[i] V[i]Z,X[i] V[i]Z[i],X[i] V[i]ZW[i],X[i]
------------------------------------------------------------------------------
1 0.99 0.99 0.99 0.99 1.00 0.99
2 0.99 0.99 0.99 0.99 1.00 0.99
Mean 0.99 0.99 0.99 0.99 1.00 0.99
------------------------------------------------------------------------------
* 0.0 means that particular PINDIS transformation was not used.
For further information about these procedures, see the
references included with these notes.